Segmentos

Segmentos

Ahora que conoces los conceptos básicos es posible usarlos para definir unos nuevos.

Imagina que en una recta se toman dos puntos distintos, digamos  y .  Entonces dicha recta queda dividida en tres regiones: dos infinitas, con orígenes en cada uno de los puntos  y , y otra finita, delimitada por los mismos.  En la siguiente imagen puedes apreciar cada una de estas regiones en diferentes colores:

A la parte finita, delimitada por los puntos  y , se le llama segmento.  A los puntos  y , que delimitan el segmento, se les conoce como puntos extremos.

Como las rectas, los segmentos suelen identificarse por medio de letras minúsculas, por ejemplo, el segmento .  Sin embargo, también se acostumbra a identificarlos escribiendo sus puntos extremos bajo una línea así: .

Medida de un segmento

Los segmentos tienen una propiedad importante: a cada uno de ellos le podemos asignar un número único, a este número se le conoce como longitud del segmento.  Es la distancia que hay entre sus extremos.

Mientras que a un segmento (de extremos ) lo identificamos así: , a su medida la representamos por el mismo símbolo pero sin la barra horizontal.  Por ejemplo, si la distancia entre los puntos  y  es  unidades, decimos que la medida del segmento  es : .

Segmentos consecutivos

Cuando dos segmentos comparten únicamente un punto extremo, se denominan segmentos consecutivos.  Si los segmentos pertenecen a una misma recta (están sobre ella), se dicen que son segmentos colineales, si no, se dicen no colineales.

En el siguiente interactivo puedes mover los puntos  y , modificando los segmentos  y .

Congruencia de segmentos

Cuando dos segmentos tienen la misma longitud se dicen que son congruentes.  Se usa el símbolo  así: si los segmentos  y  son congruentes escribimos , que se lee: “el segmento  es congruente con el segmento ”.

La congruencia de segmentos también se puede representar gráficamente: si se dibujan dos o más segmentos con una misma marca hecha en su centro, quiere decir que son congruentes.  En la siguiente figura puedes apreciar varios pares de segmentos congruentes: ,   y .

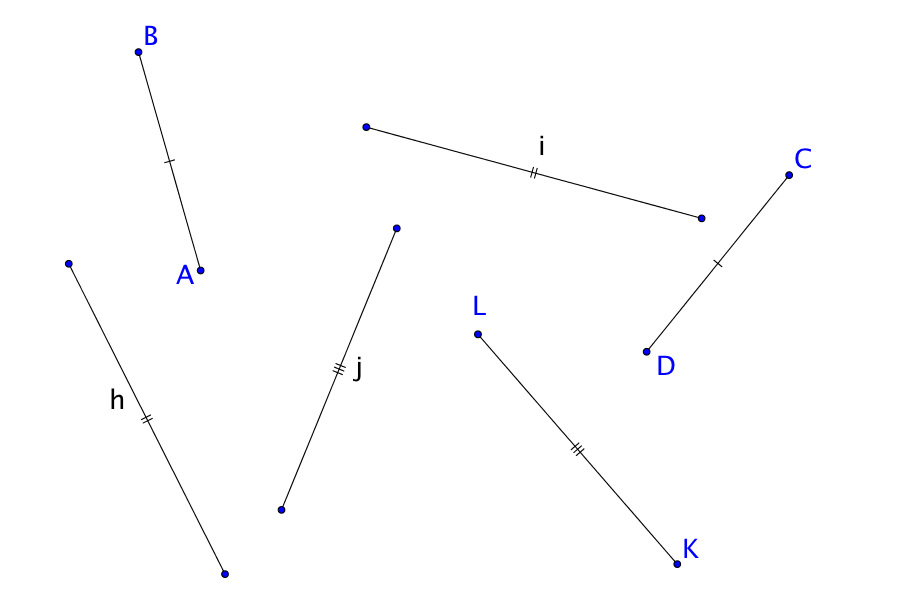
Para representar que dos segmentos no son congruentes se usa el mismo símbolo pero tachado.